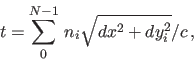Fermat's principle has to do with the path taken by a ray of
light through a (possibly inhomogeneous) medium. It states that the
path from point A to point B is the one that minimizes the light
travel time between those two points. In the case of a homogeneous
medium, that translates into the shortest distance between the two
points--a straight line--but in general it means that, if the
refractive index of the medium is 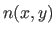 (in two dimensions, for
simplicity) then the path
(in two dimensions, for
simplicity) then the path 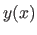 taken by the ray is the one that
minimizes
taken by the ray is the one that
minimizes
where
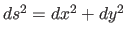 .
. 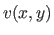 is the local speed of light
in the medium. The index of refraction,
is the local speed of light
in the medium. The index of refraction, 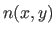 ,
gives this local speed in the medium in terms of the speed
of light in vacuum,
,
gives this local speed in the medium in terms of the speed
of light in vacuum, 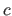 .
.
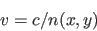 |
(1) |
In the Monte-Carlo approach to this problem, we represent the path
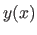 as a series of
as a series of 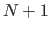 discrete points
discrete points 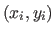 , and choose
a set of
, and choose
a set of 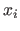 values uniformly between
values uniformly between 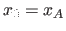 and
and 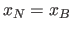 (it is
not actually necessary to choose the
(it is
not actually necessary to choose the 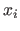 uniformly, as we will see
later). We then choose the corresponding
uniformly, as we will see
later). We then choose the corresponding 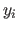 randomly, except that
randomly, except that
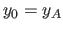 and
and 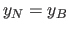 . The procedure is simple:
. The procedure is simple:
- Evaluate the quantity
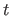 for the current configuration, as
for the current configuration, as
where
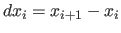 and similarly for
and similarly for 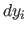 .
.
- Randomly choose one of the interior points
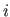 , with
, with
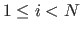 .
.
- Randomly change
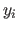 by some amount in the range
by some amount in the range ![$[-dy, dy]$](img31.png) ,
where
,
where 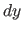 is some characteristic resolution scale of the
problem.
is some characteristic resolution scale of the
problem.
- Re-evaluate the quantity
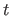 . If the random change has reduced
it from the previous value, accept the change. Otherwise,
reject it and restore the previous value of
. If the random change has reduced
it from the previous value, accept the change. Otherwise,
reject it and restore the previous value of 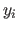 .
.
- Go back to step (1), and repeat until some large number of
trials fails to reduce
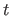 .
.
The procedure will work for any choice of 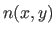 and any initial
choice of
and any initial
choice of 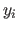 --and, in fact for any problem that can be cast in
variational form!
--and, in fact for any problem that can be cast in
variational form!
Example
Here we give details of a specific case of deriving an
optical path.
- Use Fermat's principle to determine the light path through a
transparent medium. The path starts at
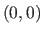 and ends at
and ends at 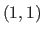 .
The refractive index of the medium is
.
The refractive index of the medium is 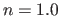 for
for 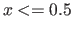 , and
, and
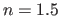 for
for 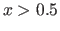 . Divide the medium into
. Divide the medium into 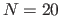 layers of equal
width and let
layers of equal
width and let
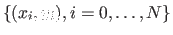 represent the path. Start
with
represent the path. Start
with 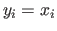 .
.
Randomly choose one value of 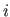 and change
and change
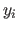 by a random number uniformly distributed in the range
by a random number uniformly distributed in the range
![$[-0.1,0.1]$](img42.png) . Accept the change if it reduces the light travel time
. Accept the change if it reduces the light travel time
where 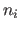 is the refractive index in layer
is the refractive index in layer 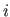 ,
, 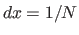 , and
, and
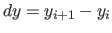 . Stop your calculation when 1000 successive trials
fail to reduce
. Stop your calculation when 1000 successive trials
fail to reduce 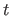 . Plot the path you obtain.
. Plot the path you obtain.
2015-02-17
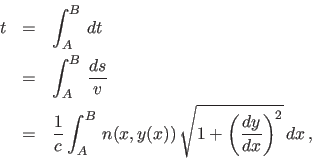
![]() as a series of
as a series of ![]() discrete points
discrete points ![]() , and choose
a set of
, and choose
a set of ![]() values uniformly between
values uniformly between ![]() and
and ![]() (it is
not actually necessary to choose the
(it is
not actually necessary to choose the ![]() uniformly, as we will see
later). We then choose the corresponding
uniformly, as we will see
later). We then choose the corresponding ![]() randomly, except that
randomly, except that
![]() and
and ![]() . The procedure is simple:
. The procedure is simple:
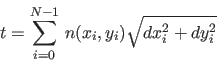
![]() and change
and change
![]() by a random number uniformly distributed in the range
by a random number uniformly distributed in the range
![]() . Accept the change if it reduces the light travel time
. Accept the change if it reduces the light travel time