Charge Distribution in a Conductor

The defining property of a conductor is that charges within it are free to move in the presence of any applied electric field. In principle, we could determine the equilibrium configuration of charges in a conductor by integrating the equations of motion of all the particles as they move under their combined electric fields. However, this is quite computationally expensive, and inefficient, since we only care about the final configuration, now how the charges got there.

We expect that the charges will redistribute themselves in such a way that no electric field exists within the conductor. Another way to say this is that the charges will move so as to minimize the total electrostatic potential of the system, subject to the constraint that the charges are confined to the conductor. We have restated the problem in terms of a variational principle -- the charges distribute themselves so as to minimize some quantity, subject to some constraint. In fact, the variational principle that the system minimizes the total electrostatic potential energy in some volume $V$

$$U = \int_V (\nabla\phi)^2\,d^3V$$

can be shown to be equivalent to Laplace's equation

$$\nabla^2\phi = 0,$$

where $\phi$ is the electrostatic potential. Monte-Carlo methods are often very well suited to problems of this type.

In two dimensions, the total potential is

$$\Phi = \sum_{i=1}^N\sum_{j=i+1}^N\, -k q_i q_j \ln r_{ij}\,,$$

where $k=9.0\times10^9$ SI units, $r_{ij} = \vert{\bf x}_i - {\bf x}_j\vert$, and $-\ln r$ (rather than $1/r$) is the fundamental electrostatic potential in 2D (think of the charges as lines of charge parallel to the $z$ axis in 3D, and recall from Physics III the calculation of the potential of two such lines). We will use the following Monte-Carlo technique to find the equilibrium configuration:

(a)

Choose a charge at random.

(b)

Randomly change both its $x$ and $y$ coordinates by amounts in the range $(-\delta,\delta)$, where we will take $\delta = 0.01$ here. If the charge would move outside the ellipse, constrain it to end up precisely on the ellipse.

(c)

Accept the above change if and only if its effect is to reduce the total potential energy of the system. Otherwise, restore the charge's old coordinates.

(d)

Repeat from (a) above. Stop when $N$ attempted changes in a row are rejected.

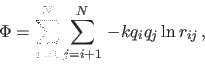
Note that the above approach is still very inefficient. You can probably think of several simple modifications that will make the program run much faster!