References:
Wilkipedia on {\em Calculus of Variations}
Fermat's Principle
We are accustomed in Physics classes to seeing the laws of Physics
stated in terms of forces, fields, and differential equations. As we
have seen, such a formulation of a problem can provide a powerful
means of obtaining the solution.
However, all of the familiar equations of elementary physics-Newton's
laws, Hamilton's equations, Maxwell's equations, and Schrödinger's,
to name a few--can equivalently be expressed in variational
form--that is, as a statement that the state of the system (or the
trajectory of a particle) is the one that minimizes some global
property, usually expressed as an integral. For example,
- Hamilton's principle states that the motion
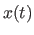 of a particle
from time
of a particle
from time 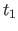 to time
to time 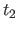 is the one that minimizes the action
is the one that minimizes the action
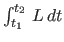 , where
, where 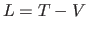 is the
Lagrangian of the system. It is easily shown that this principle is
equivalent to the Lagrangian formulation of classical mechanics.
is the
Lagrangian of the system. It is easily shown that this principle is
equivalent to the Lagrangian formulation of classical mechanics.
- The quantum-mechanical wave function
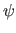 of a system with
Hamiltonian
of a system with
Hamiltonian 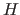 is the one that minimizes the quantity
is the one that minimizes the quantity
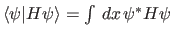 subject to
the constraint that
subject to
the constraint that
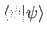 is constant. This is
equivalent to Schrödinger's equation.
is constant. This is
equivalent to Schrödinger's equation.
There are many more examples. Often, a variational formulation is the
most convenient or direct way of expressing the problem. The calculus of variations was developed precisely to handle such
problems. Here we will adopt a Monte-Carlo approach to their
solution. We will focus on two examples: Fermat's principle
(described below) and energy minimization (next). In each case, we
are seeking the configuration of a system that minimizes some
integral property of the system.
2015-02-17