Problem

A major difference between the Wave Equation and the Heat Transfer equation is that the time derivative in the LHS is of second order instead of first order. This creates a problem that we address next.

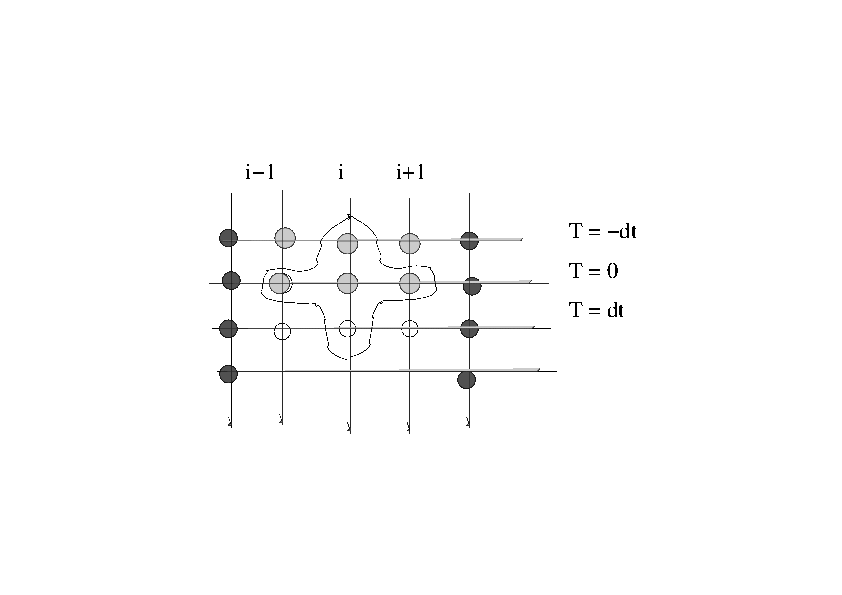
In the language of finite difference, the second time derivative mixes the solution at three time slices. That is, to predict the solution at the time $t+dt$ requires knowing the solution at two previous time slices, namely at $t$ and at $t-dt$. But, the initial value of the displacement is given only on a single time slice, not on two time slices as required.

The solution to this shortcoming is found within a clever use of the initial value. We simply have to assume that the displacement at $t=0$ is stationary. The first derivative, written in finite difference form at the initial time,

$$\frac{ \partial y }{\partial t}(x,0) = \frac{ y(x,0) - y(x,0-\Delta_t) }{\partial \Delta_t} = 0$$ (8)

then shows that the displacement at $t-dt$ is the same as that at $t=0$, $y_i^{-1} = y_i^0$. Therefore the solution becomes self starting, bootstraping the solution at later time based on the initial displacement at $t=0$.