Numerical Solution

As in the cases of the elliptic and parabolic PDEs, we derive a finite difference method to solve the Wave Equation by seeking a solution on equally spaced grids.

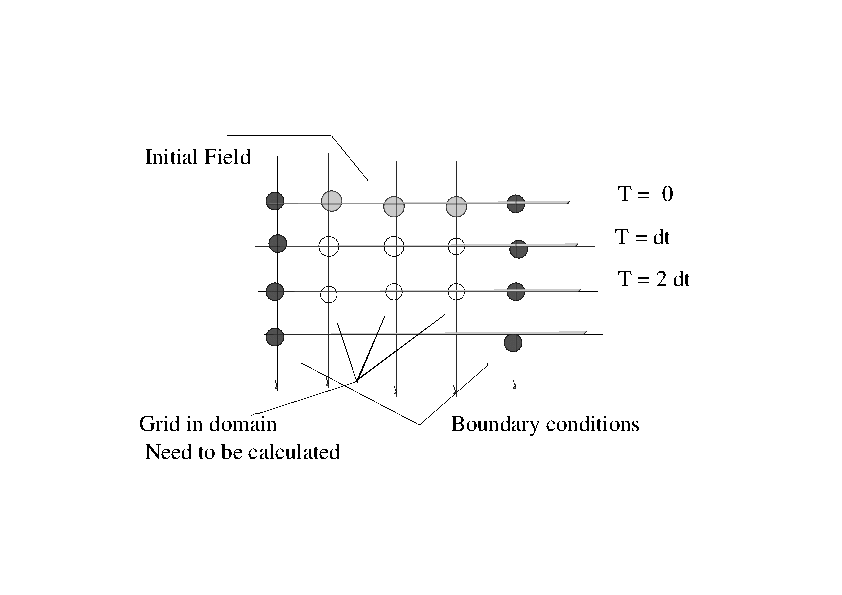
Two grid spacing's are needed, an $x$ spacing, $\Delta_x$, and a time spacing, $\Delta_t$. The grid variables are specified by $x_i , i = 0..{{N_x}-1}$ and $t_j , j = 0..N_t-1$ Note that the time grid extends to arbitrary large $N_t$. The notation for the displacement on the grid $y(x,t)$ is then $y_i^j$.

The algorithm follows from writing a finite difference version of the Wave Equation. First off, we refer back to the finite difference expressions for the derivative.

$$\left( { y^{j+1}_i + y^{j-1}_i - 2 y^j } \right) = \frac{1}... ...elta_x^2 } \left( { y^j_{i+1} + y^j_{i-1} - 2 y^j_i } \right)$$ (6)

Isolating $y(x,t)$ leads to the finite difference form of the Wave Equation.

$$y_i^{j+1} = 2 y_i^j + \frac{c^2}{c'^2} \left[ y_{i+1}^j + y_{i-1}^j -2 y_i^g \right]$$ (7)