Model

The Wave Equation is a model to describe transverse displacements of a string under tension. Assume that the tension $T$ is constant and that the string is made out of material of constant linear density, which guaranty a uniform string. Further, we will assume that the tension $T$ is sufficiently large to avoid the string sagging under gravity.

The solution of the Wave Equation is a function, $y(x,t)$, that gives the perpendicular displacement profile of the string with respect to its rest position.

The figure below illustrates an infinitesimal element of the string undergoing a perpendicular displacement.

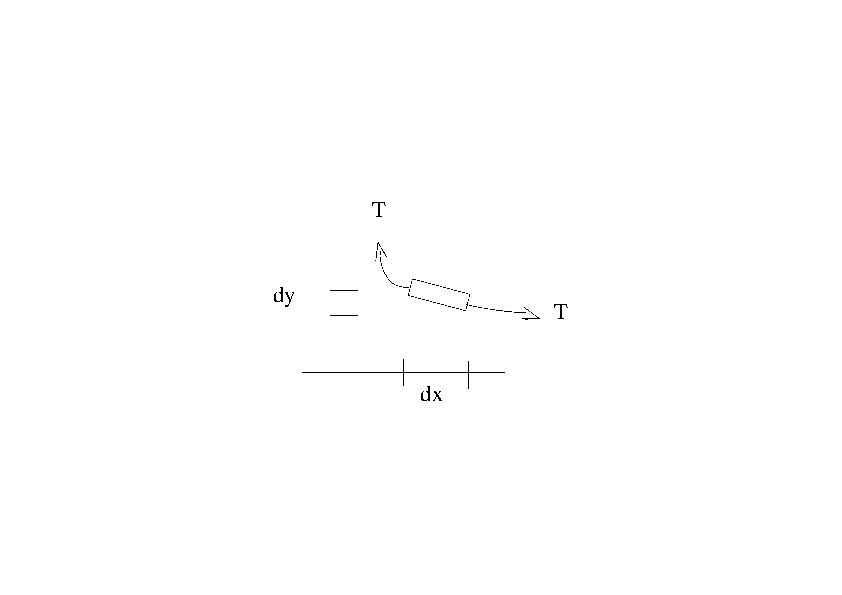
The wave equation follows from applying Newton’s equation to such a small element of the string.

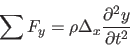$$\sum_{} F_y = \rho \Delta_x \frac{ \partial^2 y}{ \partial t^2}$$ (2)

$$\sum F_y = T \sin{ \theta(x+\Delta_x) } - T sin{ \theta(x) }$$ (3)

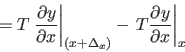$$= T \left. \frac{\partial y}{\partial x } \right\vert _{(x ... ...a_x)}- \left. T \frac{\partial y}{\partial x} \right\vert _x$$ (4)

The Wave Equation follows

$$= \frac{ \partial^2 y(x,t)}{\partial x^2} = \frac{1}{c^2} \frac{\partial^2 y(x,t)}{\partial t^2}$$ (5)

This model is over-simplified. As is, it admits an analytic solution via a separation of variables. Of course it can be made more realistic by adding, for instance, friction, gravity, ... Then the numerical solution becomes the only feasible solution.