Chaotic Solution of the Driven One Well Duffing Oscillator

Driving harder the One Well Duffing Oscillator eventually results in the system going chaotic. A characteristic of this solution is that a chaotic trajectory will fill the allowed region of phase space. The following is a sketch of a trajectory in phase space for the driven Duffing Oscillator with driving strength $A = 35.5$.

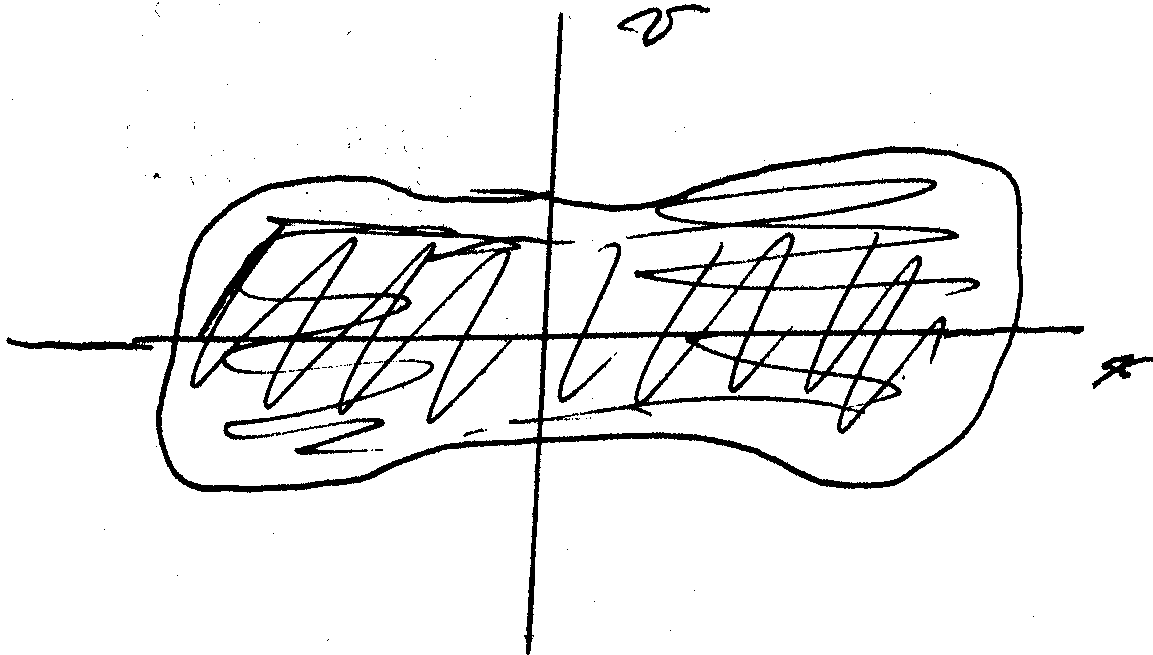
It is clear that such solution is very different that we saw previously!

Exercise #16:

Draw the phase space portrait of this solution. Use the HO setup code to feed initial conditions in the general modular RK4 ODE solver program to solve the Duffing system. Use $\alpha = 1.0$, $\beta = 1$, $\mu = 0.1$, $A = 35.5$ and $\omega = 1$ in the code. Increase the integration time ( -t 200 option) and watch for the phase space to begin to fill.

Exercise #17:

Draw the phase space again, this time starting from $(x_0,v_0) = ( 1.0,0.0)$ ( or whatever point in phase space!) and integrating over long integration times ( -t 2000 for instance ). Phase space fills again!

Order within Chaos

The solution above is chaotic. Plotting $x(t)$ and $v(t)$ versus $t$ shows that the solution has lost any trace of periodic behavior (despite the fact that the driving term is perfectly periodic!). The patterns do not repeat themselves.

The solution ventures all over the phase space but the motion remains within a finite region of space. The solution exhibits a very sensitive dependence over initial conditions - this is a hallmark of chaotic behavior.

Exercise #18:

Solve the Duffing Oscillator ( $\alpha = 1.0$, $\beta = 1$, $\mu = 0.1$, $A = 35.5$ and $\omega = 1$) starting from $(x_0,v_0) = ( 1.0,0.0)$ and integrating over long integration times ( -t 2000 for instance ). Restart the solution starting from $( x_0, v_0 ) = ( 1.00001, 0.0 )$. Plot $x(t)$ versus $t$ together for each case over increasing time intervals and watch how the two solutions diverge from each other (exponential divergence).

Stroboscopic Map - Strange Attractor

All this points to the chaotic (random) aspects of the solution. To see order within this solution requires another way of thinking. We need to look at the solution in a phase space that includes the time $t$ axis, i.e., $x(t), v(t), t$.

Exercise #19:

Plot the chaotic solution in $x(t), v(t), t$ space ( gnuplot subcommand splot ).

The system is driven by an external driving term of angular frequency $\omega = 2 \pi f = 1.0$, corresponding to a period $T = 2 \pi / \omega$. Imagine asking where is the steel beam and how fast does it go at each period of the external driving term and recording this info in a phase space like graph $v(n T)$ versus $x(n T)$. Each time $t=nT$ defines a plane in $v(n T)$ versus $x(n T)$ which the trajectory traverses at one point. So a trajectory will generate one dot per time interval $T$. This is called a Stroboscopic Surface of Section or a Stroboscopic Map.

A Limit cycle would generate very few distinguishable points in such a construct since the trajectory repeats a pattern. The chaotic solution of the Duffing Oscillator generates the following picture.

This is a Strange Attractor.

Exercise #20:

Write a Stroboscopic Code which accepts the output of the general modular RK4 ODE solver program to solve the Duffing system and outputs the values of $x(t)$, $v(t)$ and $energy(t)$ at $t=nT$. To do so find when the time has crossed $t=nT$ and perform a linear interpolation to find exact values of $x(t)$, $v(t)$ and $energy(t)$ at the crossing.

Exercise #21:

Draw the image above with 20,000 points.