Next: Chaotic Solution of the Up: Duffing_story Previous: Homoclinic Orbit
Driving the Duffing Oscillator with either ![]() or
or
![]() produces incredibly complex behavior, leading
to chaos for some range of the parameters.
produces incredibly complex behavior, leading
to chaos for some range of the parameters.
At low driving strength the one well Duffing Oscillator
exhibits attractive
Limit Cycles. This is a trajectory in phase space
toward which trajectories converge following a transient
period. The region over which initial conditions lead to
trajectories converging to the Limit Cycle is the
Basin of Attraction. The following is a sketch
of the attractive Limit Cycle for ![]() .
.
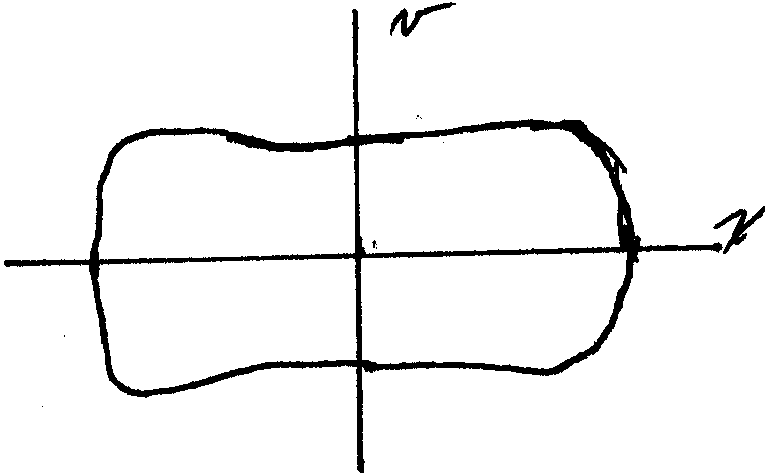
Note that the different trajectories seem to converge toward a common trajectory, a Limit Cycle
Restart the integration from suitable initial conditions for another long integration time interval to refine the Limit Cycle calculation.
Do it again, i.e., run the ODE integrator again!
Plot ![]() and
and ![]() as functions of
as functions of ![]() . Note that the period
of the Limit Cycle is that of the external forcing term.
. Note that the period
of the Limit Cycle is that of the external forcing term.
Larger Driving Strengths
Larger driving strengths can produce very different
solutions in the driven one well Duffing Oscillator. For instance
the following sketch illustrates the two
Limit Cycles at a driving
strength ![]() .
.
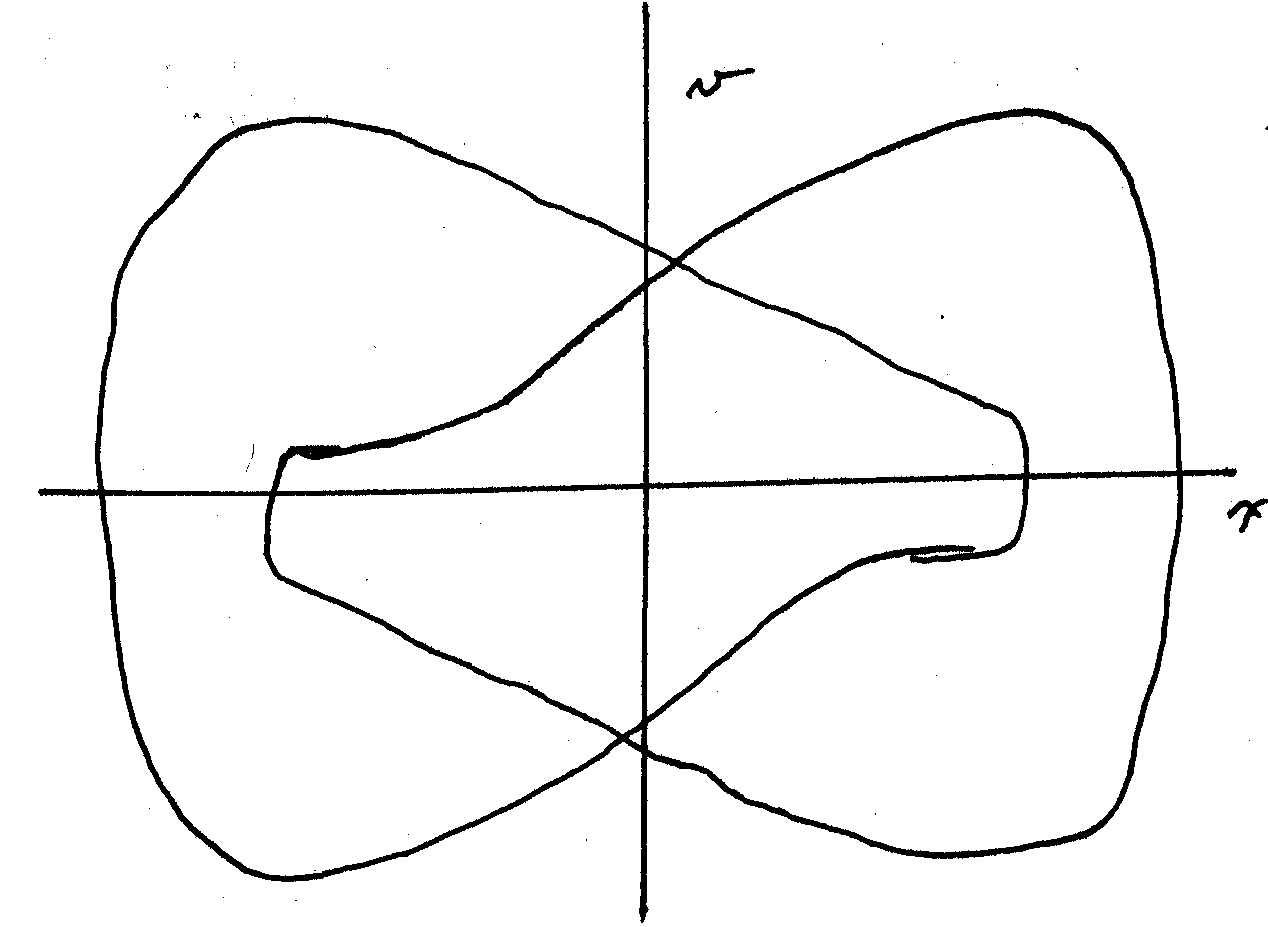
These two Limit Cycles are mirror images of each other. If a solution of a lesser symmetry than that of the potential exists, a solution of opposite symmetry should also exist.
Note that the different trajectories seem to converge toward two possible trajectories, two Limit Cycles
Restart the integration from suitable initial conditions for another long integration time interval to refine the two Limit Cycles calculations.
It is clear that each Limit Cycle has its own Basin of Attraction.
The following sketch illustrates the Limit Cycle
generated by the Duffing Oscillator driven with
a strength ![]() .
.
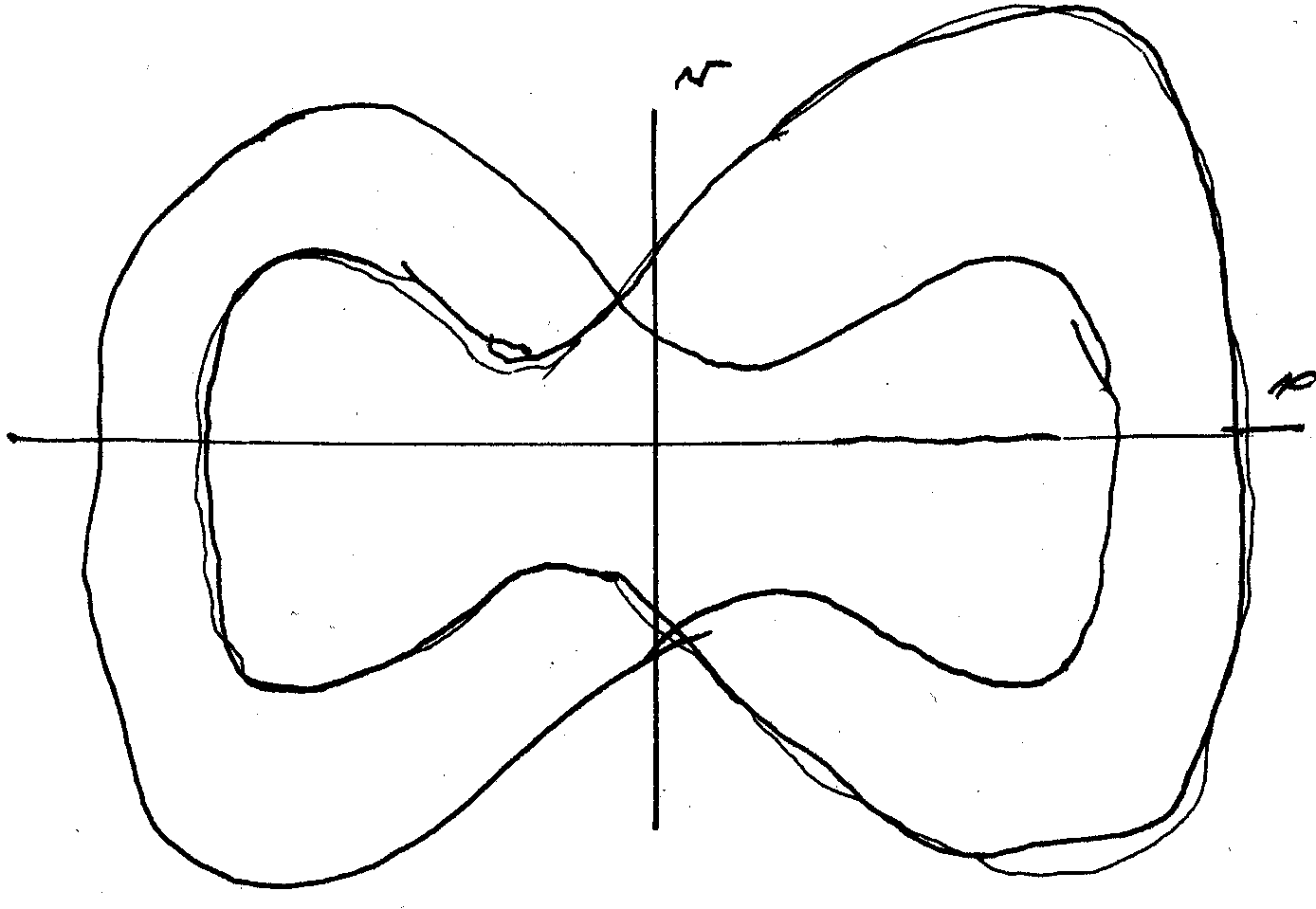
Michel Vallieres 2014-03-04