Driven Two Well Duffing Oscillator

The behavior of the Driven Two Well Duffing Oscillator is even more stunning that the Driven One Well system.

Limit Cycles

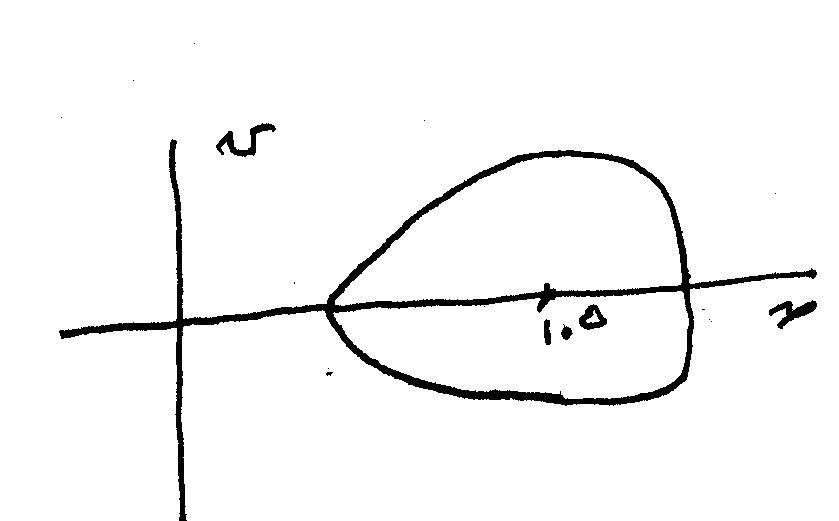
At small driving amplitudes the system stays bounded in either of the two wells and exhibits Limit Cycles. The following sketch shows the solution at driving strength $A = 0.22$. Note that the amplitude of the driving term used here is smaller than in the one well system since a new measure of strength is set by the barrier height between the two wells.

Exercise #22:

Reproduce the phase space portrait above by running the general modular RK4 ODE solver program to solve the Duffing system over long period of time ( -t 800 ) for the parameters $\alpha = 1.0$, $\beta = -1$, $\mu = 0.25$, $A = 0.22$ and $\omega = 1$ starting at initial conditions $(x_0,v_0) = ( 1.0,0.0)$.

Exercise #23:

Refine the image of the Limit Cycle.

Transient Chaos

At larger driving amplitudes the system may traverse from one well to the other. At not such a high driving strength, the systems exhibits temporarily a chaotic behavior before settling in a Limit Cycle. This is called transient chaos.

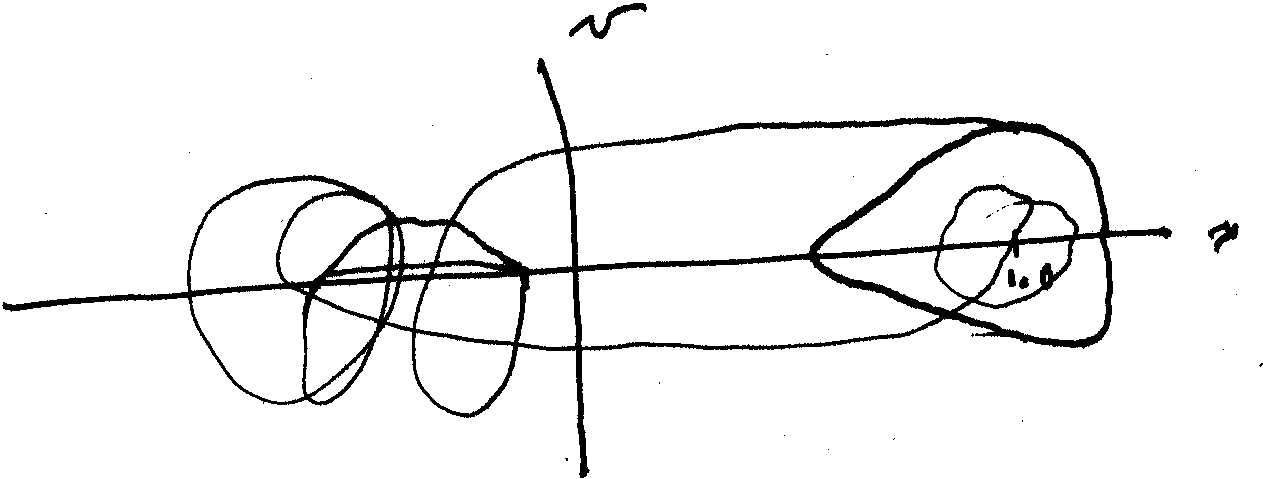
The following sketch shows the solution at driving strength $A = 0.245$.

Exercise #24:

Reproduce the phase space portrait above by running the general modular RK4 ODE solver program to solve the Duffing system over long period of time ( -t 800 ) for the parameters $\alpha = 1.0$, $\beta = -1$, $\mu = 0.25$, $A = 0.245$ and $\omega = 1$.

Exercise #25:

Plot $x(t)$ versus $t$ in the transient time period to illustrate the oscillations from one well to the other, a characteristic of the chaotic behavior.

Exercise #26:

Refine the image of the Limit Cycle.

Chaos

At larger yet driving amplitudes the system has an easier time traversing from one minimum to the other. The system may then become chaotic. A characteristic of the chaoticity will then be for the steel beam to bounce from one well to another in an erratic manner.

As in the case of the one well system, the solution now fills in the phase space.

Only a stroboscopic surface of section can reveal the order in this solution.

Exercise #27:

Reproduce the stroboscopic surface of section above by running the general modular RK4 ODE solver program to solve the Duffing system over long period of time ( -t 2000 ) for the parameters $\alpha = 1.0$, $\beta = -1$, $\mu = 0.25$, $A = 0.4$ and $\omega = 1$ and piping the results in the stroboscopic code. Use initial conditions $x_0 = 1.0$ and $v_0 = 0.0$.

Exercise #28:

Plot $x(t)$ versus $t$ over small time periods to illustrate the oscillations from one well to the other, a characteristic of the chaotic behavior.

Exercise #29:

Refine the image of the stroboscopic surface of section.

Exercise #30:

Start from different initial conditions; what happens to the figure formed in the stroboscopic surface of section.