Modified Harmonic Oscillator - One Well System

Setting $\alpha = 1.0$ (usual value in standard analysis of the model) changes the potential well shape.

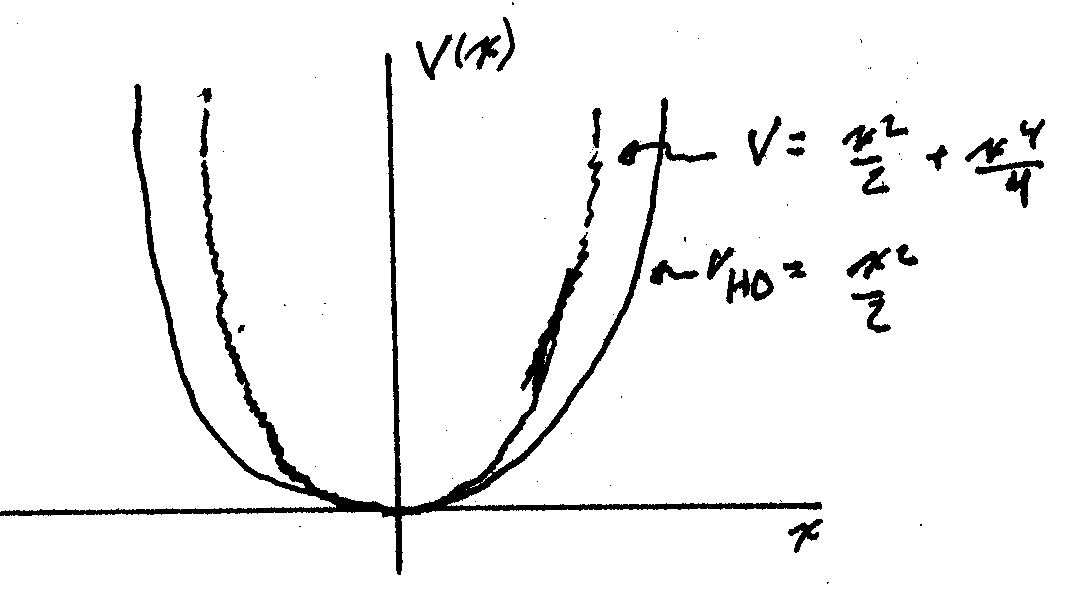
This changes the shape of the phase space portrait. The extra stiffness of the beam squares the trajectories by imparting a stronger impact on the beam to push it in opposite direction than the force resulting from a parabolic potential by itself could have.

Exercise #3:

Reproduce the phase space portrait as obtained for the HO in the previous exercises. Use the HO setup code to specify the initial conditions. Use the general modular RK4 ODE solver program to solve the Duffing system. Use $\alpha = 1.0$, $\beta = 1$, $\mu = 0.0$, $A = 0.0$ and $\omega = 1$ in the code.

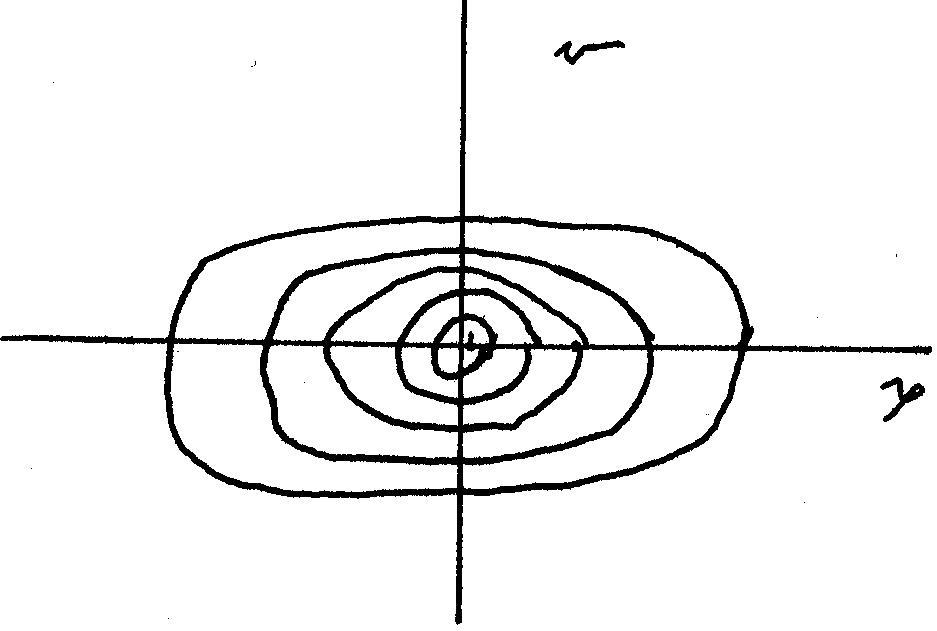
Dissipative System

The phase space portrait with $\mu$ not zero shows that the origin, $x = 0$, $v = 0$ remains an attractive equilibrium point or fixed point. This point makes the RHS of the ODEs equal to zero. It corresponds to a minimum energy point. Trajectories spiral toward this fixed point.

Exercise #4:

Reproduce the phase space portrait above by using initial conditions generated by the HO setup code. Use $\alpha = 1.0$, $\beta = 1$, $\mu = 0.1$, $A = 0.0$ and $\omega = 1$ in the code implementing the RK4 solution of Duffing Oscillator.

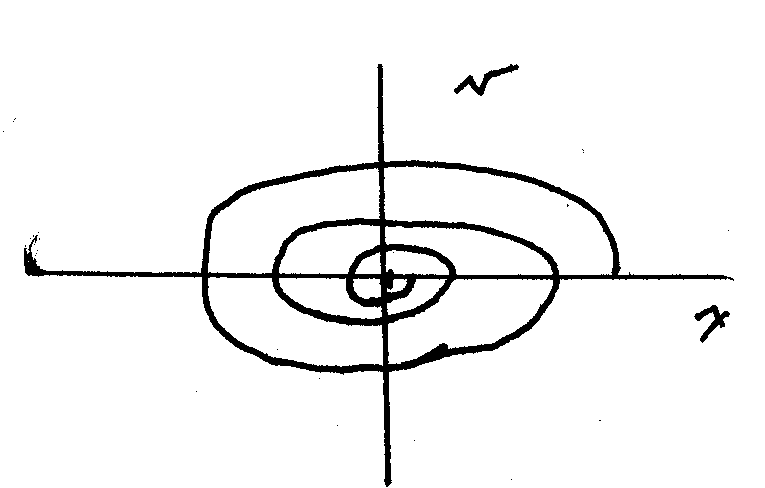
Plot the energy corresponding to each of the initial conditions used in building the phase space portrait above. Note the energy dissipation.