Next: Homoclinic Orbit Up: Duffing_story Previous: Modified Harmonic Oscillator -
Setting ![]() dramatically
changes the shape of the potential.
It becomes a Two Wells Potential.
dramatically
changes the shape of the potential.
It becomes a Two Wells Potential.
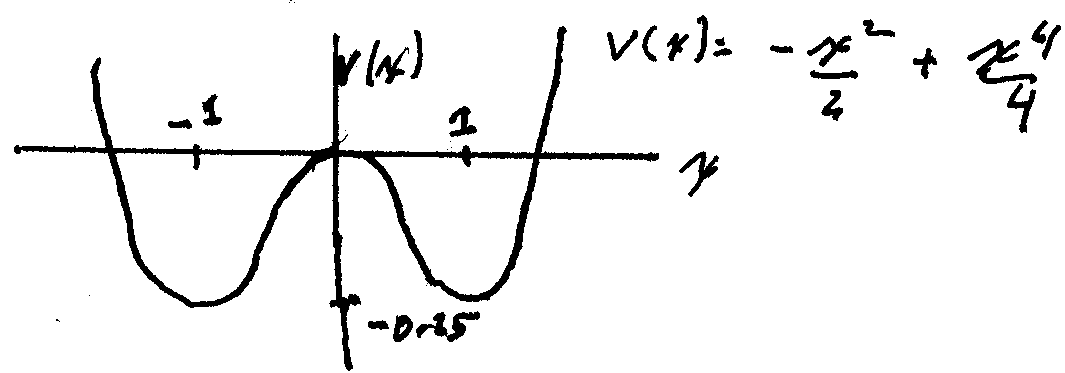
This potential harbors two minima at ![]() = +1 and -1 (
= +1 and -1 ( ![]() ) and
a maximum at
) and
a maximum at ![]() . The phase space portrait of the solution
of this problem is very different than that of the single well
problem.
. The phase space portrait of the solution
of this problem is very different than that of the single well
problem.
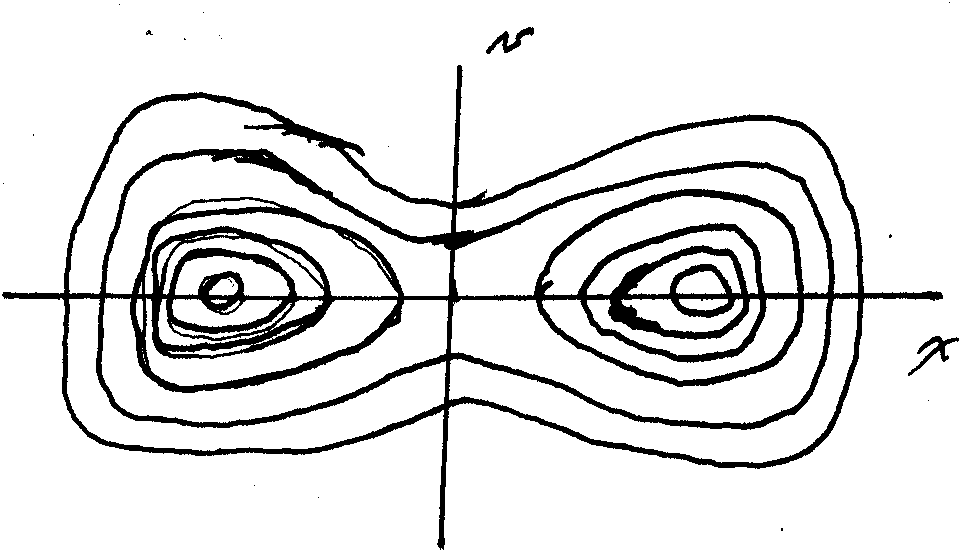
Use ![]() ,
, ![]() ,
,
![]() ,
, ![]() and
and ![]() in the
code implementing the RK4 solution of Duffing Oscillator.
in the
code implementing the RK4 solution of Duffing Oscillator.
Check that the energy is conserved, i.e., constant, for each trajectory.