Harmonic Oscillator Limit

Harmonic Oscillator limit - $\beta = 1$ case

With $\beta = 1$ and $\alpha, \mu, A$ all equal to zero this system is a simple harmonic oscillator (mass=1).

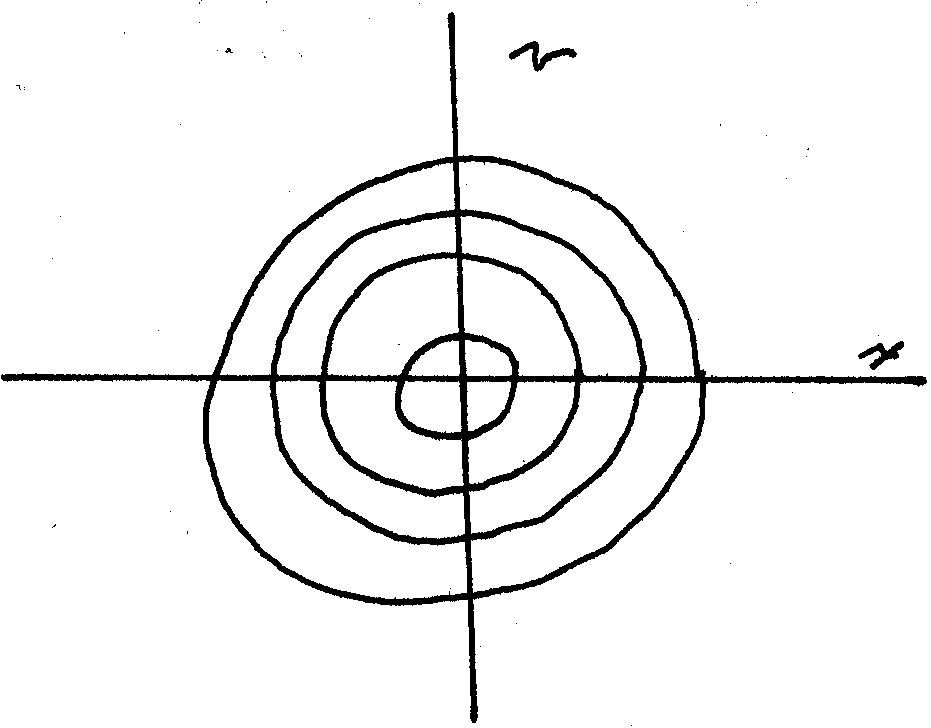
The solution of the model produces a phase space portrait in $v(t)$ versus $x(t)$ of simple concentric circles surrounding the Fixed Point at the origin. The Fixed Point of a set of ODEs is at coordinates that render the RHS of the ODEs equal to zero.

Exercise #1:

This system is a harmonic oscillator. Draw the phase space portrait of this solution. You should write a HO setup code to feed initial conditions in the ODE solver code. The program should sprinkle initial conditions along the positive $x$ axis. The latter must be written with a program control ( -i ) to control whether or not to read in initial conditions from <stdin>.

Use the general modular RK4 ODE solver program to solve the Duffing system, using $\alpha =0.0$, $\beta = 1$, $\mu = 0.0$, $A = 0.0$ and $\omega = 1$ in the code. Use $dt = 0.02$.

Check that the energy of each trajectory is conserved by the numerical solution.

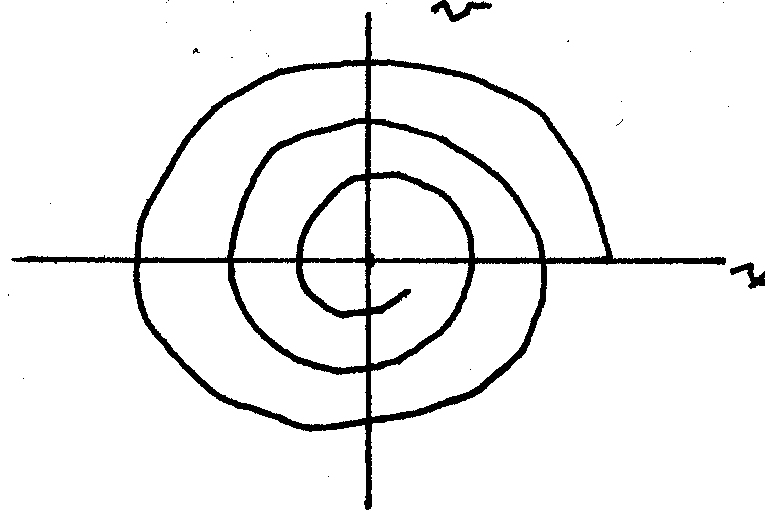
Dissipative System

With $\mu$ not zero, the system becomes a damped harmonic oscillator. This term takes energy away from the motion of the steel beam. All trajectories spiral into the attractive Fixed Point at the origin.

Exercise #2:

Draw the phase space portrait of this solution. Use the HO setup code to feed initial conditions in the general modular RK4 ODE solver program to solve the Duffing system. Use $\alpha =0.0$, $\beta = 1$, $\mu = 0.1$, $A = 0.0$ and $\omega = 1$ in the code.

Plot the energy of the system along these trajectories as functions of time.

Note the energy dissipation.