Exact solution of the Ising Model

Onsager solved the Ising model analytically through a fantastic application of mathematical physics.

Energy

$$E = - N_s J \coth(2J) \left[ 1 + \frac{2}{\pi} \kappa' K_1(\kappa) \right]$$

Magnetization

$$M = \pm N_s \frac{ ( 1+z^2)^{1/4} (1-6 z^2 + z^4 )^{1/8} } { ( 1-z^2)^{1/2} }$$

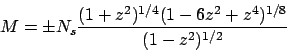
Specific heat

$$C_B = N_s \frac{2}{\pi} ( J \coth(2J) )^2 \left( 2 K_1(\ka... ...) \left[ \frac{\pi}{2} + \kappa' K_1(\kappa) \right] \right)$$

$z$, $\kappa$ and $\kappa'$ are

$$z = exp(- 2 J)$$

$$\kappa = 2 \frac{ \sinh(2 J ) } { \cosh^2( 2 J ) }$$

$$\kappa' = 2 \tanh^2( 2 J ) - 1$$

The elliptic functions are

$$K_1(\kappa) \equiv \int_{0}^{\pi/2} \frac{ d \phi } { ( 1 - \kappa^2 \sin^2( \phi) )^{1/2} }$$

$$E_1(\kappa) \equiv \int_{0}^{\pi/2} d \phi ( 1 - \kappa^2 \sin^2( \phi) )^{1/2}$$

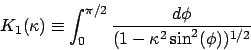
The analytical solution of the model in 3D is not known, and it may be impossible to derive.