The Ising Model in Two Dimensions

The Ising model in two dimension is a model for a magnetic material. It consist of classical spins on a equally spaced lattice in 2 dimensions. Basic statistical physics will be used to computer the properties of such a model at temperature $T$.

The model consists of a set of spin degree of freedom interacting with each other and with an external magnetic field. For example, these spins could represent the magnetic moments of the atoms in a solid. The spins are located on a 2D lattice of size $N_s = N_x N_y$. Each spin is labeled by $S_\alpha = S_{ij}$, where $i$ and $j$ refer to the position on the lattice, and $\alpha$ is a generic site label. These spins are assumed classical (i.e., not following quantum mechanics rules) and assumed to be spin $\frac{1}{2}$. Therefore each spin is pointing up ($S_\alpha=+1$) or down ($S_\alpha=-1$).

The energy of the system is written

$$E(S) \equiv H(S) = - J' \sum_{ < \alpha \beta > } S_\alpha S_\beta - B' \sum_\alpha S_\alpha$$

The notation $< \alpha \beta >$ means that the sum is over the nearest neighbor pairs of spin. The spin at site $i,j$ interacts with spins at $i \pm 1, j$ and $i, j \pm 1$ with strength $J'$. Each spin could also interact with an external magnetic field of strength $B'$.

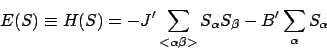
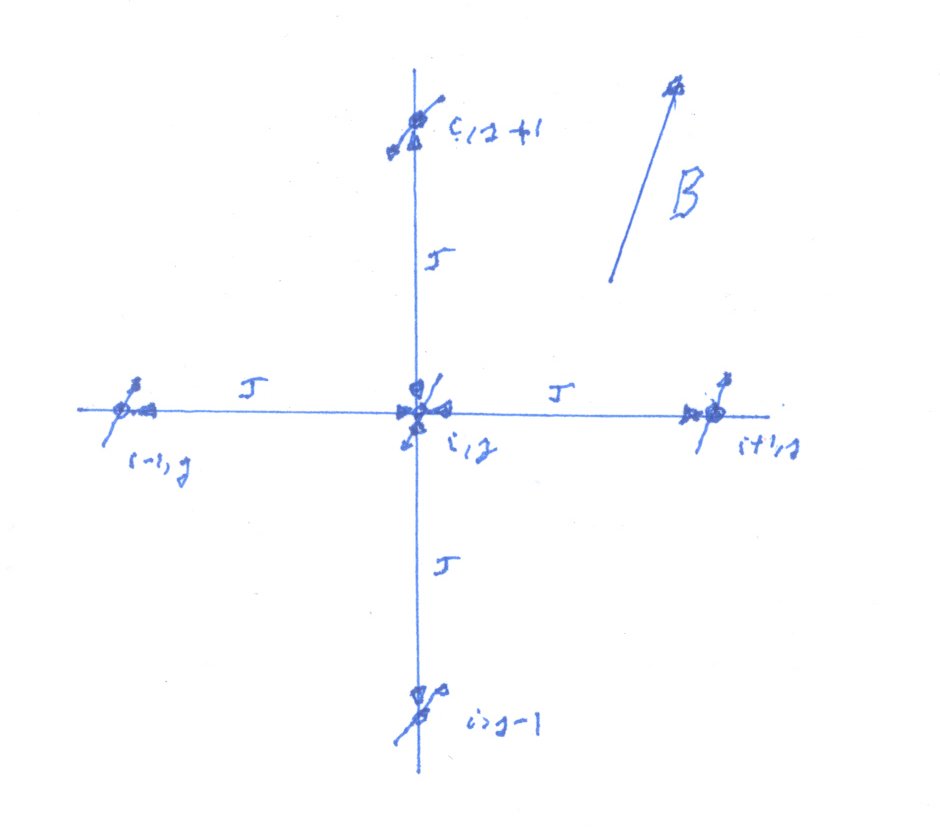
Periodic boundary conditions are applied. The neighbor of a spin on the left of the lattice is taken as the spin on the right of the lattice and vice versa for the spin on the right. The same applies for the spins at sites at the bottom and the top of the lattice. These boundary conditions model a system of infinite dimensions. The topology of the lattice is therefore that of torus.

If $J$ is positive the energy favors the parallel spin between neighbors, this is ferromagnetism. If $J$ is negative, the spin will tend to be anti-aligned or antiferromagnetism.

Any system in statistical equilibrium at temperature $T$ is such that all possible configurations of the systems may occur with probabilities

$$w(S) = \frac{ \exp( - \frac{ H(S) }{ k T } ) }{ Z }$$

where the partition function $Z$

$$Z( J', B' ) = \sum_{ S } \exp( - \frac{ H(S) }{ k T } )$$

normalizes $w(S)$. $T$ is the temperature in absolute degree and $k$ the Boltzman constant. For our calculation it is convenient to scale the strength of the interaction $J=\frac{J'}{kT}$ and of the magnetic field $B=\frac{B'}{kT}$ in terms of the factor $kT$. Therefore high temperature will correspond to small $J$ and $B$ while at low temperature $J$ and $B$ will be large.

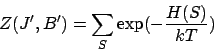
The energy of the system depends on the $N_s = N_x N_y$ spins on the lattice. Each spin can be in two possible configurations, $\pm 1$. The total number of configurations is then $2^{N_s}$. This is an enormous number of terms to perform sums over. A very modest lattices of $20,20$ corresponds to a number of configurations $2^{400}$. Therefore the sums have to be done via Monte Carlo sampling. Note that these sums take the role of the integrals we described in previous sections.

The needed sums are based on the simple statistics idea of averaging the given variables over the probabilities. The energy of the system is therefore

$$E = \sum_S w(S) H(S)$$

The magnetization is

$$M = \sum_S w(S) \left( \sum_\alpha S_\alpha \right)$$

The specific heat at constant field is

$$C_B = \sum_S w(S) H^2(S) - E^2$$

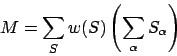
The program ising.c implements this solution. It uses Monte Carlo sampling obtained via the Metropolis et al algorithm based on the probability of the spin configurations to calculate the energy and magnetization of the system.

The code defaults to a 20 X 20 lattice. It samples phase space by flipping the spins at random. The issue becomes that of the step size as we discussed before. In this case the choice is to flip spins or not to flip spins. Flipping all the spins on the lattice at once would likely lead to a step that is too large; configurations would be missed in the sampling. The code uses the idea of a sweep of the lattice where spins are systematically flipped from site to site on the entire lattice with the proviso that each trial flip be accepted or rejected according to the Metropolis algorithm. This is found by experience to be a more effective way of sampling.

It also leads to an efficient way of calculating the ratio of probability between the trial and the previous spin configuration. The acceptance of the trial step depends on the ratio of the weight function.

$$r = \frac{ w(X_t) } { w(X_n) } \equiv e^{-H(S_t) + H(S) }$$

When only one spin is flipped the ratio of the exponential of the energy depends only on the neighbors spins. The ratio takes the form

$$r = e^{ -2 S_\alpha( J f + B ) }$$

where

$$f = S_{i+1,j} + S_{i-1,j} + S_{i,j+1} + S_{i,j-1}$$

The $f$ factor can only take 5 different values, namely $0, \pm 1, \pm 2, \pm4$. Only 10 values of $r$ can occur. This makes for a very efficient coding by storing the exponential factors ahead of time.

Another interesting question is to know when to stop sampling? This question is answered in the code by a special way of doing statistic. Sampling is done at every NFREQ sweeps. These sweeps are binned into groups with NSIZE members. For each group the mean and the standard deviations are calculated. Groups values for the average are then considered to be independent variables and a grand average is calculated. The standard deviation of this grand average can be calculated via the standard variance formula for the different averages of the groups or via the average of the variances of the groups. When sufficient sampling is accomplished, these two results should be the same. This provides a measure of goodness of the sampling.