Next: The Metropolis Et Al Up: Monte_Carlo_story Previous: The Monte Carlo Integration
The Monte Carlo Integration Method can be improved greatly by
a nonuniform sampling if variations in the integrand ![]() are smooth.
are smooth.
Multiply and divide the integrand ![]() by a
positive weight function
by a
positive weight function ![]()
The integral now becomes
The Monte Carlo evaluation of ![]() proceeds as before, e.g., averaging
the values of f(x) divided by
proceeds as before, e.g., averaging
the values of f(x) divided by ![]() via a random sampling of points
uniformally distributed in
via a random sampling of points
uniformally distributed in ![]() in the interval [0,1], namely
in the interval [0,1], namely
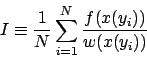
If ![]() has the same smooth variation as
has the same smooth variation as ![]() , e.g.,
, e.g., ![]() is large or small where
is large or small where ![]() is large or small, the ratio
is large or small, the ratio ![]() will be
roughly a constant over the interval [0, 1]. This ought to improve the
accuracy in calculating the integral.
will be
roughly a constant over the interval [0, 1]. This ought to improve the
accuracy in calculating the integral.
There is a fundamentaly different interpretation of the
the results that we have just obtained.
The change of variable in differential form
We will see in the next subsection a method to generate random numbers of arbitrary distribution. This will become a fundamental tool to evaluate multi-dimensional integrals.
Michel Vallieres 2014-04-01