The Model

We will study the scattering in two dimensions of a mass $m$ on three repellor potential mounds.

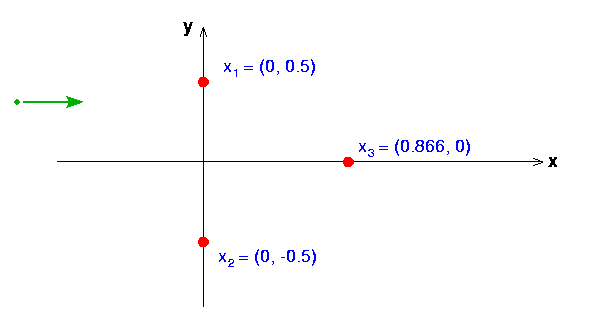
The three force centers are located at (static) positions $\vec{x}_j, j = 1, 2, 3$. For definiteness, take the three repellors to be identical and lying on the vertices of an equilateral triangle: $\vec{x}_{1,2} = (0, \pm\frac12)$, $\vec{x}_3 = (\frac12\sqrt3, 0)$.

Each of these potential repellors is

$$\phi_j = {\textstyle\frac12}kb^2 e^{-r_j^2/b^2}$$

where $\vec{r}_j \equiv \vec{x} - \vec{x}_j$, $r_j = \vert\vec{r}_j\vert$, and $b$ and $k$ set the scale and strength, respectively, of the interaction. Note that, as defined, $k$ has dimensions $T^{-2}$.

The C code potential.c calls the function total energy() to calculate the total energy of the particle (for the parameters as in Exercise 1 below). It yields the potential energy if the velocity of the particle is zero. You can use gnuplot (sub command splot) to visualize the potential repellors. The function total_energy() in this code could be included in your numerical scattering problem solution in response to the exercises below. Here is the resulting picture:

The total acceleration $a = - \frac{1}{m} \frac{d V}{d x}$ is given by a contribution from each repellor. Using $m=1$,

$$\vec{a} = \sum_{j=1}^3 \vec{a}_j ,$$

where the $j$-th partial acceleration due to the $j$-th repellor is

$$\vec{a}_j = k e^{-r_j^2/b^2} \vec{r}_j .$$

Solving the 4 dimensional system of ODEs that results will yield the trajectory of the particle among the potential repellors.

Numerical Solution of the Scattering Model

The Runge-Kutta 4th order can be used to solve Newton's equation. Note that the equations are describing motion in 2 dimensions, i.e., Newton's equation leads to a 4 dimensional system to solve.

Use a time step $\delta t = \eta$, where $\eta$ is a parameter which may be adjusted to control the overall accuracy of the calculation. This step should depend on $k$ as well, as in $\delta t = \eta/\sqrt{k}$.

Rather than focusing on individual trajectories, we will instead look at a scattering problem--that is, we imagine probing the potential near the origin by firing a beam of particles of known energy into it, and noting how their properties are changed when they finally leave the interaction region. Let's choose our beam to start at the left-hand side of the figure, at $x_0=-4$, moving to the right with some speed $v_0$, which we will hold fixed for the duration of the experiment. Thus, the initial condition for an individual scattering trajectory is

$$\vec{x}_0 = (-4, y_0), \vec{v}_0 = (v_0, 0) .$$

The distance $y_0$ from the $x$ axis is the impact parameter.

Since the particle always has positive energy, we expect it to eventually escape. For $v_0 < \sqrt{k/m} b$ , the particle can never penetrate any of the potentials--it always ``bounces off.''

Note that we only need consider $y_0 \ge 0$, by symmetry.