The Monte Carlo Integration Strategy

We will first look at an integral in one dimension to learn about the Monte Carlo Method. Of course the method is normally used to evaluate multi-dimensional integrals.

Consider an integral over $x$ in a domain [0,1].

$$I = \int_{0}^{1} f(x) dx$$

An alternative to the Trapezoidal or Simpson Integration Rules is reached by thinking of $I$ as resulting from the product of the average of $f(x)$ over the domain by the volume of the domain. Therefore $I$ can be approximated as

$$I \equiv \frac{1}{N} \sum_{i=1}^{N} f( x_i)$$

$I$ is therefore proportional the average of $f(x)$ using a set of points $x_i$. A possible choice of points $x_i$ could be random positions with equal probability everywhere within the domain [0,1].

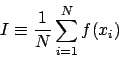
The uncertainty associated with this evaluation of the integral is given by the variance in calculating the average of $f(x)$, namely

$$\sigma^2 = \frac{1}{N} < ( f(x) - < f(x) > )^2 >$$

or

$$\sigma^2 = \frac{1}{N} ( < f^2(x) > - < f(x) >^2 )$$

or

$$\sigma^2 = \frac{1}{N} \left[ \frac{1}{N} \sum_{i=1}^{N} f_i^2 - \left( \frac{1}{N} \sum_{i=1}^{N} f_i \right)^2 \right]$$

$\sigma$ measures the extent to which $f(x)$ deviates from its average value over the region of integration.

The calculation of $\sigma$ reveals two important aspects of the Monte Carlo Integration. First, the uncertainty in the estimate of the integral decreases as $N^{-1/2}$. If more points are used to calculate $I$, better the answer will be. But this is by far a slower convergence than the traditional Trapezoidal or Simpson Rules that go as $1/N$ or $1/N^2$.

The second aspect that $\sigma$ reveals is that the error in calculating the integral depends on the fluctuations in $f(x)$. For $f(x)$ constant, a small number of $N$ (1 value) would be enough to calculate the average accurately. On the other hand, a very peaked $f(x)$ would be poorly represented by sampling with equally distributed random numbers and would therefore produce a very poor value of the integral.