Integrable Systems - Order

An important class of potential based two-dimensional motion are those that are integrable. For these systems there exists a second conserved quantity, a constant of the motion, constraining the trajectory to a two dimensional manifold in the four dimensional phase space. Two familiar kinds of such integrable systems are those based on the separable and central potentials.

In the separable potential case the potential is the sum of two independent functions of $x$ and $y$ respectively, $V(x,y)=V_x(x)+V_y(y)$. This leads to two conserved quantities, $E_x$ and $E_y$, the energies in $x$ and $y$ motions respectively. The trajectories in $x$ and $y$ decouple from each other, each behaving as one-dimensional motion. Each of these motions trace concentric ellipses, or concentric deformed contours, in the $x, p_x$ and $y, p_y$ independent two-dimensional phase spaces.

The solutions of these problems can be derived analytically by combining two one-dimensional solutions obtained by techniques from classical mechanics.

The total energy $E = E_x + E_y$ is a constant. Assume that $V_{x,y}$ have a minimum (zero value) at particular values of $x$ and $y$ respectively. Fig. 2.1 shows schematically trajectories (labeled A to E) with energies from 0 to $E$. Therefore the trajectories in the $x, p_x$ and $y, p_y$ subspaces combine to describe the trajectories of the particle in 4-dimensional phase space.

From another point of view, the concentric closed contours in Fig. 2.1 result from the intersections of the full trajectories with the appropriate plane. They are called Surfaces of Section (SOS). The concentric closed contours are the hallmark of integrability.

The central potential case

$$V(x,y) = V_r(r) , r = \sqrt{x^2 + y^2}$$

leads to the angular momentum, $L = m ( x v_y - y v_x )$ as the second conserved quantity. The trajectories are again constrained to be on a two-dimensional manifold in the four-dimensional phase space.

Although the dynamics of integrable systems are simple, it is often not easy to make this simplicity apparent. The trajectories remain in four-dimensional phase space despite being restricted to two-dimensional manifolds. We can deduce hints about the topology of the latter by considering a central potential. The total energy of such a system can be written as

$$E = K_{radial} + K_{angular} + V(r)$$

The energy in the angular motion is $K_{angular} = \frac{L^2}{2 m r^2}$. For constant $E$ and $L$, the radial motion is bounded between two turning points (where $K_{radial} = 0$), $r_{in}$ and $r_{out}$, which are the solutions of

$$E - V(r) - \frac{L^2}{2 m r^2} = 0$$

For any $r_{in} < r < r_{out}$ the radial kinetic energy is $K_{radial} = E - K_{angular} - V(r)$, which sets the radial velocity $\pm v_r(r)$. Thus the two-dimensional manifold on which these trajectories reside has the topology of a torus.

A $y, v_y$ SOS, built by recording $y$ and $v_y$ each time that $x = 0$ along the trajectory, should show closed contours. Recall that $v_r$ is $v_y$ on this SOS. Changing $E$ or $L$ will change the dimension of the torus and therefore will also change the contours in the SOS.

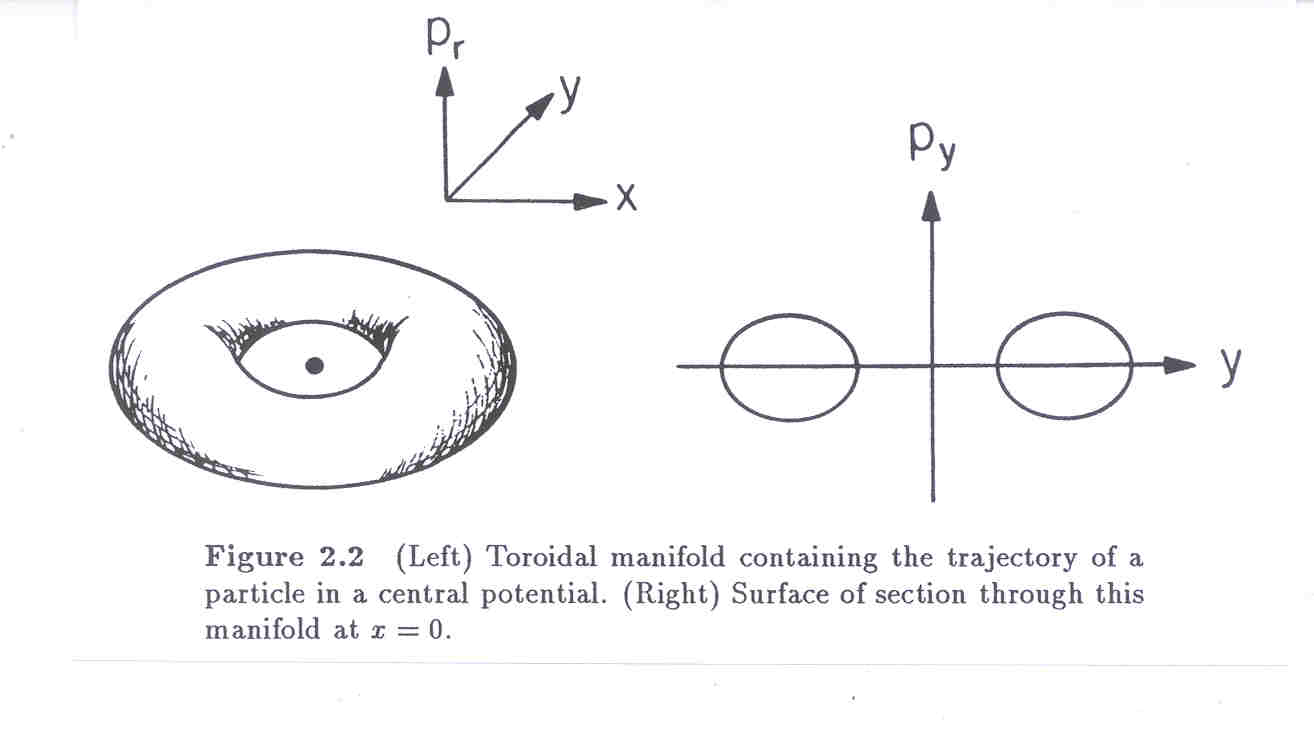
The toroidal topology of the phase space of a central potential can be shown to characterize all integrable systems. The manifold on which lies a trajectory with given constants of the motion is called an Invariant Torus. There are many of these for a given energy. The SOS might schematically look like the following:

There are fixed points associated with trajectories that repeat exactly after some period. The elliptic fixed points organize stable trajectories under perturbations. Around each of these there is a family of concentric tori, bounded by a separatrix. The hyperbolic fixed points occur at the intersections of separatrices. They are stable under perturbation along one of the axis of the hyperbola, but unstable along the other.