It ha been found that the long scattering orbits
(large scattering times) are those that come
in the neighborhood of periodic orbits. These scattering trajectories spend time
close to unstable periodic orbits before going away since these periodic
orbits are unstable.
Finding periodic orbits in open systems (chaotic scattering) or closed
systems is notoriously difficult. This is particularly the case for
unstable periodic orbits. Tracking these orbits is difficult since any
slight deviation from the true orbit will take the trajectory away from the
true one by definition of an unstable orbit.
The search for periodic orbits in a chaotic region can proceed via
various ways.
- Visually look for region where a chaotic trajectory seems to stay
in the neighborhood of a periodic orbit. This may point out to a set of
initial conditions from which to start a brute force search.
- Perform a brute force search. This is done via launching numerous
trajectories from a grid of initial conditions and recognizing which of
these trajectories close on themselves. This is difficult and time
consuming in high dimensional systems.
- Recently (2000), Henry, Watt and Wearne proposed a lattice refinement
technique to find periodic orbits and demonstrated the usefulness of
the method for Maps and Flows. The
original paper
or a
local copy
are available in pdf format.
The C code
search_for_orbits.c
implements the lattice refinement search
algorithm for the Three Hills Potential
used as scatterer above.
The salient features of the code are
- It is based on a RK4 solution of the scattering problem - the
calculation of scattering trajectories is the same as the calculation
of a periodic orbit
- The solution of the ODEs is in a separate C function (ODE_solve) for clarity
- ODE_solve assumes initial conditions of the type (
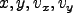 ) =
(
) =
(
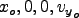 )
)
- ODE_solve computes the trajectory until a point
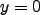 is reached
with the constraint that
is reached
with the constraint that 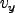 be of the same sign
as the initial
be of the same sign
as the initial 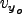 for the first time or for hits times.
This defines a Poincare Surface of Section (SoS).
for the first time or for hits times.
This defines a Poincare Surface of Section (SoS).
- This choice for the SoS exploits +y / -y symmetry of the potential function.
Other choices ae possible.
- ODE_solve sharpens the coordinates of the point of
intersection of the trajectory with the
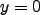 plane via
a linear interpolation.
plane via
a linear interpolation.
- The function search
implements the search algorithm from a grid of initial conditions covering
(
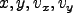 ) = (
) = (
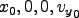 )
)
- This search function is recursively called to refine the search when any of the
4 projected crossings from the vertices of each cell on the search
lattice fall within the same cell. These projections are calculated
via affine projections as proposed by Henry et Al..
The output of the code are suggestions for sets of initial conditions
that should result in periodic orbits.
Michel Vallieres
2011-02-02