D(f)
D[i](f)
f
- expression which can be applied as a function
i
- positive integer or expression or sequence of such
·
Given f, a function of one argument, the call D(f) computes the
derivative of the function f. For example, D(sin) returns cos. The derivative is
a function of one argument such that D(f)(x) = diff(f(x), x). That is, D(f) =
unapply(diff(f(x), x), x). Thus D is a mapping from unary functions to unary
functions.
·
Given f, a function of n arguments, the call D[i](f) computes the
partial derivative of f with respect to its ith argument. More generally,
D[i,j](f) is equivalent to D[i](D[j](f)), and D[](f) = f. Thus D[i] is a mapping
from n-ary functions to n-ary functions.
·
The argument f must be an algebraic expression which can be
treated as a function. It may contain constants, known function names (such as
exp, sin), unknown function names (such as f, g), arrow operators (such as x
-> x^2), and the arithmetic and functional operators. For example, f+g, f*g,
and f@g are valid since (f+g)(x) = f(x)+g(x), (f*g)(x) = f(x)*g(x), and (f@g)(x)
= f(g(x)), where f@g denotes functional composition.
·
The usual rules for differentiation hold. In addition, it is
assumed that partial derivatives commute. Hence D(f+g) = D(f) + D(g), D(f*g) =
D(g*f) = D(f)*g + D(g)*f, D(f@g) = D(f)@g * D(g), D[i,j](f) = D[j,i](f), and so
forth.
·
IMPORTANT: composition of functions f and g is denoted by f@g NOT
f(g). D(sin(y)) is wrong; use D(sin@y).
·
To specify that a symbol a is a constant and not a function, use
assume(a,constant). Then D will understand that D(a) is 0 and D(sin(a)*f) is
sin(a)*D(f).
·
For a comparison of D and diff see operators[D].
·
The D operator can also compute partial derivatives of functions
which are defined as procedures. This is known as automatic differentiation. The
function f can be a Maple procedure which has assignments to local variables, if
statements, for loops, while loops, etc. See the examples.
> D(sin);
![]()
> D(exp+cos^2+Pi+tan);
![]()
> D(ln);
![]()
> D(ln)(x)
= diff(ln(x),x);
![]()
> D(f);
![]()
> D(f)(0);
# the first derivative of f evaluated at 0
![]()
> D(D(f));
![]()
> (D@@2)(f);
![]()
> (D@@n)(f);
![]()
> D(f@g);
# the derivative of the composition of two functions
![]()
> D(sin(y));
# this does not mean sin composed with y
![]()
> D(sin@y);
![]()
> D(2*sin(a)*f);
![]()
> assume(a,constant);
D(2*sin(a)*f);
![]()
> D[](f);
![]()
> D[i](f);
![]()
> D[i$n](f);
![]()
> D[i,j](f);
![]()
> D[i,j](f)-D[j,i](f);
![]()
> D[1](D[2,1](f));
![]()
> D[i](D[j,i](f));
![]()
> f
:= x -> x^2;
![]()
> D(f);
![]()
> f
:= (x,y) -> exp(x*y);
![]()
> D[](f);
![]()
> D[1](f);
![]()
> D[2](f);
![]()
> f
:= x -> g(x,y(x));
![]()
> D(f);
![]()
> f
:= proc(x) local t1,t2;
t1 := x^2;
t2
:= sin(x);
3*t1*t2+2*x*t1-x*t2
end
proc:
Compute the derivative of f with respect to f's first
argument x
> D(f);
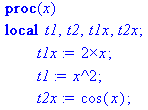
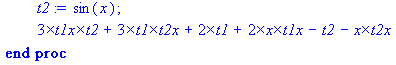
Check that the procedure computes the derivative correctly
> D(f)(x)
- diff(f(x),x);
![]()
> f
:= proc(x,b,n) local i,s;
s := 0;
for
i from n by -1 to 0 do s := s*x+b[i] end do;
s
end
proc:
The procedure f above evaluates a polynomial b at x using
Horners rule. The polynomial b is input as an array of coefficients array(0..n).
> D[1](f);
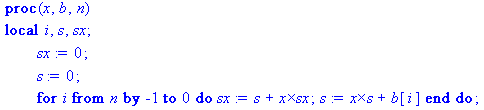
![]()
diff, @,
@@, unapply,
operators, taylor,
operators[D]
|
Any questions or suggestions should be directed to |