- problem set-up
- choice of parameters: v0 = 0.2, eps = 0.0, step = 0.05, t = 0,...,100
- energy conservation: plot dE as a function of time
- precession: print times and angles of successive maximum separations
- orbital elements: semimajor axis and eccentricity
(where E is the relative orbital energy per unit mass, M is the total mass, and h is the relative orbital angular momentum per unit mass)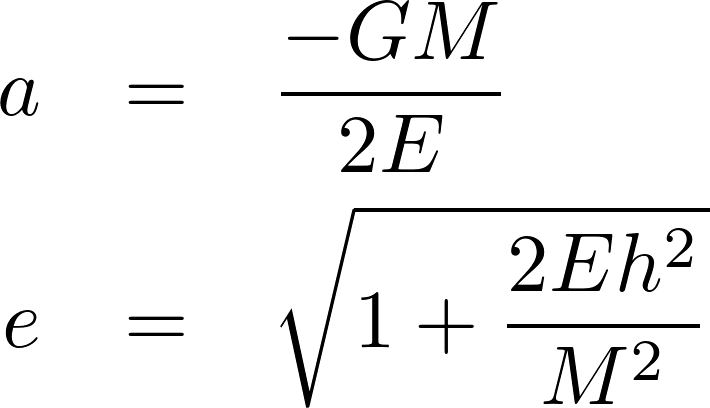
- plot both as functions of time
- solution
- problem set-up: Sun + Earth + "Jupiter," circular orbits
- choose eps = 0.0
- initial conditions:
- Sun: particle 0, mass ms = 1.0, pos = [0, 0, 0], vel = [0, 0, 0]
- Earth: particle 1, mass = 3.e-6, pos = [1, 0, 0],
vel = [0, ve, 0],
where ve^2 = G (ms+me)/re - Jupiter: particle 2, mass mj = 0.01, pos =
[0, rj, 0], vel = [-vj, 0, 0],
where vj^2 = G (ms+mj)/rj - start Earth and Jupiter at the same phase on their respective orbits, on the x-axis
- transform to the center of mass frame before starting the integration (useful for visualization)
- run with step = 0.01 to time t_end = 1000
- plot Earth's semimajor axis and eccentricity as functions of time
- STOP if semimajor axis < 0 (unbound orbit)
- find the maximum Earth eccentricity over the course of the run
- run with (i) mj = 0.01, rj = 3.0, (ii) mj = 0.02, rj = 2.1, (iii) mj = 0.03, rj = 2.0
- Here is a starting point.
- solution