The Shooting Method

Boundary-value problems are more difficult to solve than initial-value problems. Simply put, you don't have all the information you need to start at one side of the range ( x = a ), then compute the trajectory using a standard integrator (Midpoint or Runge-Kutta-4, for example) until you reach the other side ( x = b ). Some of the necessary initial conditions are unknown.

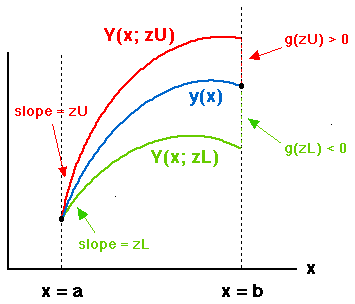
One popular and easily understood approach to this problem is known as shooting. In essence, you fire a series of trial ``shots'' (that is, you perform a series of initial-value calculations) across the range [ a, b ], guessing any initial conditions (at x = a ) that are not specified, and refining your guesses until the boundary conditions at x = b are satisfied.

The method is easiest to describe in the two-dimensional case N = 2, with the component $~y_1~$ specified at each end of the range. For definiteness, let's imagine that we are really solving a second-order system, so $~y_2~$ is the derivative of $~y_1~$. The procedure is as follows. For definiteness, we will denote the true solution of the boundary-value problem by y, and will use Y to denote numerical solutions.

1. Fixing the initial value of $Y_1 = y_1 = \alpha_1$ at x = a, and denoting by z the guess of the unknown value of $Y_2 = y_2$ there, integrate numerically across the range a < x < b to obtain a numerical estimate of $Y_1(b)$. Define the error, that is, the mismatch between the numerical result and the required boundary condition, to be $g(z) = Y_1(b) - \beta_1$:
   

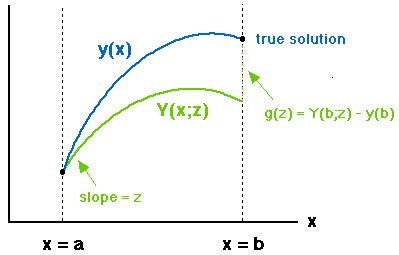
   Solving the boundary-value problem then amounts to solving the equation g(z) = 0.

2. Perform a series of trial integrations until two values of z are found with $g(z_L) < 0$ and $g(z_U) > 0$:
   

3. Since we expect g to be a continuous function of z, and since we know that any solution we find is unique, we can now simply iterate by bisection (or otherwise) to find the value of z that solves the problem.