The simplest way to solve an algebraic equation of the form g(z) =
0, for some function g is known as bisection.
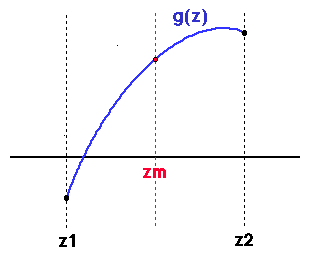
The method assumes that we start with two values of z that
bracket a root: z1 (to the left) and z2 (to the
right), say. Then, we iteratively narrow the range as follows.
First, define zm to be the midpoint of the range: zm =
(z1 + z2)/2. Then, if g(zm) has the same sign as
g(z1), and assuming that there is only one root in the range,
then we know that the root must lie in [zm,z2], and we can
replace z1 by zm. If not, then the root lies in
[z1,zm], so zm can replace z2.

if (g(zm)*g(z1) > 0) z1 = zm; else z2 = zm;
The process continues until |z2-z1| becomes less than some specified tolerance. Obviously, the uncertainty in the value of the root (the width of the range) decreases by a factor of two with each iteration, that is, we gain approximately 1 decimal digit of accuracy every 3 iterations.
Of course, finding the initial range [z1,z2] may not be a
simple task. We will return to this later.
The bisection method relies solely on the assumption that the function
g is continuous, so its value at the midpoint
(eventually) lies between its values at the end of the range. If
g is differentiable, we can do better. In that
case, a straight-line approximation to g in the range
[z1,z2] is appropriate, and we can estimate the root by
linear interpolation (or extrapolation). After each iteration, the
range is refined to incorporate the improved information.
In the secant method, we always use zs and the previous
estimate of the root (z2 say):
Generally speaking, these methods work best when we are already
close to the solution. One can construct situations where the secant
method performs far worse than bisection but, as a rule of
thumb, it can be shown that, once we are close to a root, the secant
method more than doubles the number of digits of accuracy of
the answer every two iterations. False position, while
slower, still converges substantially faster than bisection.
Very often, we start a root-finding exercise by using bisection,
because that method, while relatively slow to converge, is very
stable. However, it is common to perform a couple of secant
iterations at the end of the process, once we are fairly close to the
solution, to ``refine'' the results and gain a great deal more
accuracy.
The most efficient method for finding a root of an equation is known
as Newton-Raphson. In this method, instead of doing linear
interpolation between two points known to straddle the root, as in the
secant method, we use the value of the function g and its
derivative g' at some point z, and simply
follow the tangent to the point where it crosses the axis.
When it can be used, Newton-Raphson converges extremely rapidly.
In fact, the number of digits of accuracy doubles at each
iteration. However, the method requires that we know g',
which may not always be the case (for example, if g is known
only as a tabulated or numerically defined function). Note, though,
that it is possible to make numerical estimates of g' by
evaluating g at two nearby points. The method also suffers
from the fact that it can be wildly unstable if we start far from the
root (for example, if we started at the point labeled z2 in
the earlier figures, Newton Raphson would send us off in entirely the
wrong direction). And of course, if happen to land near a turning
point, where g'(z) = 0, the method will fail badly.
Like the secant method, Newton-Raphson is often used to refine our
results after bisection has already brought us fairly close to the
desired solution.
The False-Position and Secant Methods
In C, we can write:
zs = z1 + (z2 - z1) * (-g(z1)) / (g(z2) - g(z1));
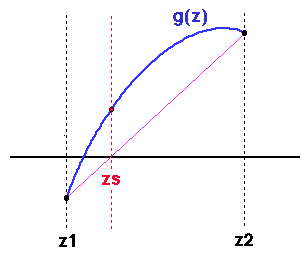
Both the false-position and the secant methods use
this approach. The difference between the two is simply what you so
with the information once you have it. In the method of false
position (sometimes called regula falsi), we refine our range
so that [z1,z2] always spans the root, as with
bisection. That is, we replace z1 or z2 by
zs depending on the sign of g(zs):
/* False position iteration. */
zs = z1 + (z2 - z1) * (-g(z1)) / (g(z2) - g(z1));
if (g(zs)*g(z1) > 0)
z1 = zs;
else
z2 = zs;
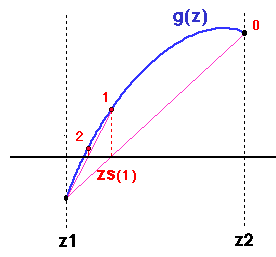
/* Secant iteration. */
zs = z1 + (z2 - z1) * (-g(z1)) / (g(z2) - g(z1));
z1 = z2;
z2 = zs;
Note that, with false position, we are guaranteed that our range
always spans the root, and convergence is assured, although the method
is generally slower than the secant method. Specifically, in the
configuration shown above, the iterates would approach the solution
from the right, leaving z1 unchanged and slowing the
convergence. As illustrated below, with the secant scheme, the root
may not remain bracketed, and there is always the possiblilty of an
instability causing the method to fail. (This is usually not a
problem if we are close to the root and g is almost linear
in [z1,z2], but it is a real possibility if the function has
several ``wiggles'' in the range.)
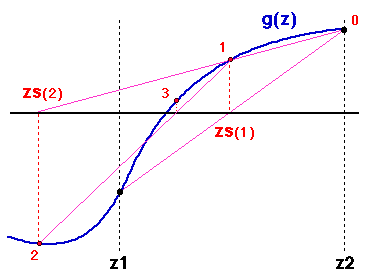
The Newton-Raphson Method
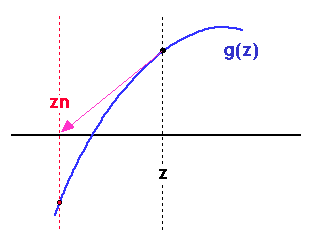
Obviously, zn = z - g(z)/g'(z). In this example, you can see
that the next iteration (starting at zn) will already bring
us very close to the root.