Making a Boundary-Value Solver
Assume that we have at our disposal two programs -- one
(midpoint.cc) to solve a
initial-value problem using the midpoint method, the other
(bisect.cc) to solve the
equation g(z) = 0 using bisection (possibly with one or more
secant refinements at the end). We can combine them to solve simple
boundary-value problems in a very straightforward way.
As remarked earlier, for the simple
two-point boundary problem for a two-dimensional (e.g. second-order)
system with the same component 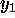 specified at each end of the range, we can regard the IV integrator as
a means of mapping our guess z of the unknown slope at the
left-hand end of the range into the error g(z) (that is, the
amount by which we ``miss'' the proper boundary condition at the
right-hand side). Thus, all we need to do is to turn
the main function of the integrator into the
function g used by the root finder, then proceed as before to
solve for the root of g. Note that, in this case, we know
that there is a single unique root.
specified at each end of the range, we can regard the IV integrator as
a means of mapping our guess z of the unknown slope at the
left-hand end of the range into the error g(z) (that is, the
amount by which we ``miss'' the proper boundary condition at the
right-hand side). Thus, all we need to do is to turn
the main function of the integrator into the
function g used by the root finder, then proceed as before to
solve for the root of g. Note that, in this case, we know
that there is a single unique root.
The main program and the initialize function of
the integrator are
void initialize(double y[], double& x, double& dx, double& x_max)
{
// Specify initial conditions.
x = 0;
y[0] = 0;
y[1] = 1;
dx = 0.01;
x_max = 1;
}
void main()
{
double y[N], x, dx, x_max;
initialize(y, x, dx, x_max);
while (!time_to_stop(y, x, x_max)) {
output(y, x);
step(y, x, dx);
}
output(y, x);
}
(Note the usual C/C++ awkwardness that y[0] here refers to
the first component of the dependent
variable, 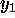 , and so on.)
, and so on.)
We want to repackage these functions to create the function
g, whose single argument z specifies the initial
value of y[1] and whose return value is the error y[0] -
BETA. Thus we need to pass the value of z to
initialize, and modify the program slightly, as follows (the
modified lines are marked):
void initialize(double y[], double& x, double& dx,
double& x_max, double z) // <====
{
// Specify initial conditions.
x = 0;
y[0] = ALPHA; // <====
y[1] = z; // <====
dx = 0.01;
x_max = 1;
}
double g(double z) // <====
{
double y[N], x, dx, x_max;
initialize(y, x, dx, x_max, z); // <====
while (!time_to_stop(y, x, x_max)) {
output(y, x);
step(y, &x, dx);
}
output(y, x);
return y[0] - BETA; // <====
}
It is assumed that the boundary values of y[0], ALPHA and BETA, are
specified (perhaps by a #define statement) elsewhere in the
program.
That's all there is to it! Nothing else in the merged program
needs to be changed.
Here is the complete program, set up to solve
the system of equations:
dy[0]/dx = y[1],
dy[1]/dx = -W*y[0]
(so the system is just the harmonic oscillator problem y'' + Wy = 0),
with boundary conditions
y[0] = ALPHA at x = XMIN
y[0] = BETA at x = XMAX
We take W = 1, XMIN = 0, XMAX = 1,
ALPHA = 1, and BETA = 2. The only embellishments
are the inclusion of both midpoint and Runge-Kutta-4 integrators, and
the use of a simple root-bracketing function bracket_root
prior to beginning the bisection process:
#define FAC 1.5
void bracket_root(double& zl, double& zr)
{
int id = 0;
zl = -0.5; // Initial range
zr = -zl;
// Expand the range by alternately increasing zl and zr by a
// factor FAC. Note that this is only guaranteed to work if
// the system is known to have a SINGLE root.
while (g(zl)*g(zr) > 0) {
zl *= FAC;
id = 1;
if (g(zl)*g(zr) > 0) {
zr *= FAC;
id = 2;
}
}
// Now we know which increase was successful in bracketing
// the root: id = 1 <==> zl; id = 2 <==> zr.
if (id == 1)
zr = zl/FAC;
else
zl = zr/FAC;
}
Because there is a single root, bracketing is relatively easy in this
case.
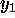 specified at each end of the range, we can regard the IV integrator as
a means of mapping our guess z of the unknown slope at the
left-hand end of the range into the error g(z) (that is, the
amount by which we ``miss'' the proper boundary condition at the
right-hand side). Thus, all we need to do is to turn
the main function of the integrator into the
function g used by the root finder, then proceed as before to
solve for the root of g. Note that, in this case, we know
that there is a single unique root.
specified at each end of the range, we can regard the IV integrator as
a means of mapping our guess z of the unknown slope at the
left-hand end of the range into the error g(z) (that is, the
amount by which we ``miss'' the proper boundary condition at the
right-hand side). Thus, all we need to do is to turn
the main function of the integrator into the
function g used by the root finder, then proceed as before to
solve for the root of g. Note that, in this case, we know
that there is a single unique root.