Tips for Answering Questions

Some questions can be answered two ways. You can use Newton's form of K3 and find the radius in m, mass in kg and calculate the period in seconds. OR you can use what I did in class:

In all the questions you can assume that the mass of the satellite << the mass of earth or the mass of the planet << mass of the sun (star) so M1 + M2 = M1 = M

Therefore

$$P^2 = \frac{4 \pi^2 a^3}{ G M}$$ (4)

rearranging the equation you get

$$\frac{P^2 M}{a^3} = \frac{4 \pi^2}{G} = {\rm constant value}$$ (5)

This holds for ANY system, satellite orbiting earth, planet round star etc and allows you to relate one system to another as

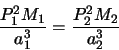$$\frac{P^2_1 M_1}{a^3_1} = \frac{P^2_2 M_2}{a^3_2}$$ (6)

Then providing that P₁ has the same units as P₂, M₁ has the same units as M₂ and a₁ has the same units as a₂ it doesn't matter what the units are.

e.g. A satellite is orbiting the Earth in a geostationary orbit (it orbits once every 24 hours). If the satellite is moved to double the distance, what is it's new period?

Let us relate the new system (denoted by the 2's) to the first system which is the satellite orbiting the earth in 24 hours. We know that M₂ = M₁ as the satellite is still orbiting the Earth. a₂ = 2a₁ (given in question) and P₂ is what we want to find. Then

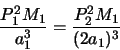$$\frac{P^2_1 M_1}{a^3_1} = \frac{P^2_2 M_1}{(2a_1)^3}$$ (7)

The M's and a's cancel leaving

P₁² = P₂²/8 (8)

so that

$$P_2 = \sqrt{8} P_1$$ (9)

but we know P₁ is 24 hours so P₂ =$\sqrt{8}$ 24 hours = 68 hours.