

Next: About this document ...
Up: Energy I: Week 3
Previous: Energy I: Week 3
Electrical circuits are more good examples of oscillatory behavior.
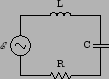
The general circuit we want to consider looks like
which, going counter-clockwise around the circuit gives the loop
equation
where 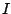 is the current in the circuit, and
is the current in the circuit, and 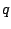 the charge on the
capacitor as a function of time.
the charge on the
capacitor as a function of time.
We note that 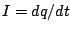 and
and
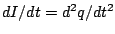 , so that our equation becomes
, so that our equation becomes
and we will first look the undriven case 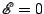 . This gives
the following equation
. This gives
the following equation
which should be familiar - a second degree ordinary differential
equation with constant coefficients. We saw this same equation when
we studied damped motion. In fact, this is the same equation and
describes essentially the same phenomenon. Let us compare:
It doesn't take long to see that the equations are identical with the
following correspondence:
where we simply compare term-by-term. NOTE that it is the capacitor
that corresponds to the spring not the inductor, even though the
picture of an inductor looks like a spring!
So, charge is like displacement, inductance like mass (inertia),
resistance like damping, and capacitance like compliance (inverse
springiness). Now that we have the variable correspondence we can
write down the solution by comparison:
So the behavior of our circuit is characterized by damped oscillations
of the charge on the capacitor.
Note that when we have no resistance (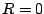 ), our equation simplifies
to
), our equation simplifies
to
which is the equation for simple harmonic motion with frequency
Now, it is in general very difficult to solve this equation when
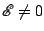 . An important method is the Laplace Transform,
which turns our differential equation into an algebraic one, which is
(hopefully) easier to solve. Conceptually you get the following:
. An important method is the Laplace Transform,
which turns our differential equation into an algebraic one, which is
(hopefully) easier to solve. Conceptually you get the following:
where 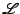 stands for the Laplace transform and
stands for the Laplace transform and
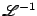 its inverse. In any case, if we take a sinusoidal
emf
its inverse. In any case, if we take a sinusoidal
emf
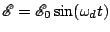 , then the above
procedure tells us that we obtain a state of resonance in the circuit
when
, then the above
procedure tells us that we obtain a state of resonance in the circuit
when
where
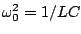 , which is just a little bit different from
what we'd expect. The stuff on the right is the 'natural frequency' of
the circuit, but we're going to assume that
, which is just a little bit different from
what we'd expect. The stuff on the right is the 'natural frequency' of
the circuit, but we're going to assume that 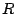 is small enough that
the resonance frequency is simply given by
is small enough that
the resonance frequency is simply given by 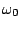 . How small?
Well, we need that second frequency in the above equation to be very
small compared to the first, or
. How small?
Well, we need that second frequency in the above equation to be very
small compared to the first, or
which, when solved for 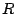 gives
gives
since
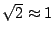 (order of magnitude). We will even assume
(order of magnitude). We will even assume
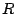 to be 'small' so that we can solve for it nicely in one problem.
It's a good idea to go back, after finding
to be 'small' so that we can solve for it nicely in one problem.
It's a good idea to go back, after finding 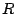 , to make sure it
actually does satisfy this condition, otherwise the assumption was
wrong and our value of
, to make sure it
actually does satisfy this condition, otherwise the assumption was
wrong and our value of 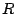 is no good!
is no good!


Next: About this document ...
Up: Energy I: Week 3
Previous: Energy I: Week 3
Dan Cross
2006-10-17

![]() and
and
![]() , so that our equation becomes
, so that our equation becomes
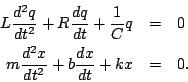
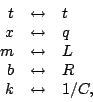
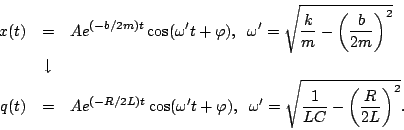
![]() ), our equation simplifies
to
), our equation simplifies
to
![]() . An important method is the Laplace Transform,
which turns our differential equation into an algebraic one, which is
(hopefully) easier to solve. Conceptually you get the following:
. An important method is the Laplace Transform,
which turns our differential equation into an algebraic one, which is
(hopefully) easier to solve. Conceptually you get the following: